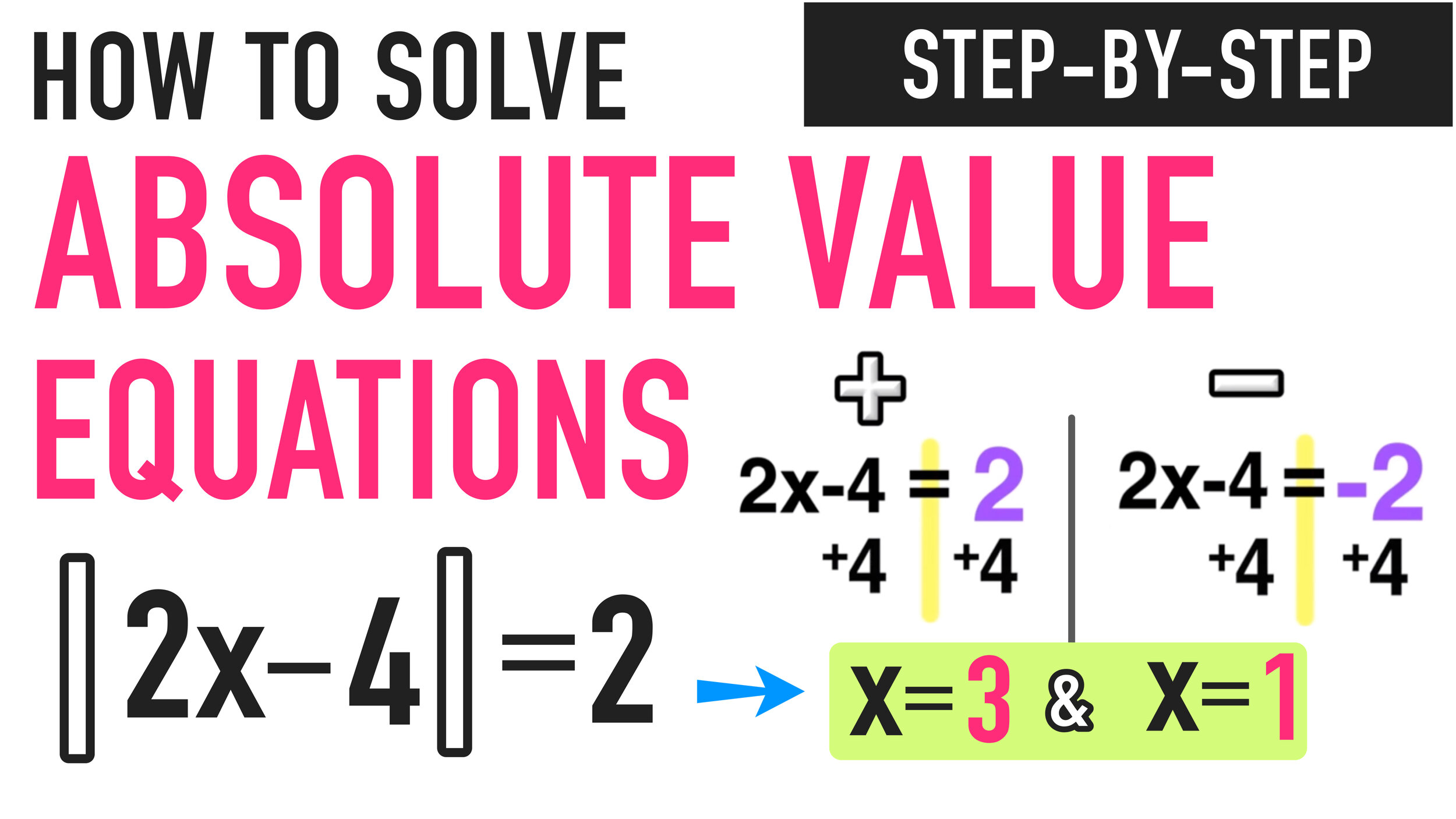
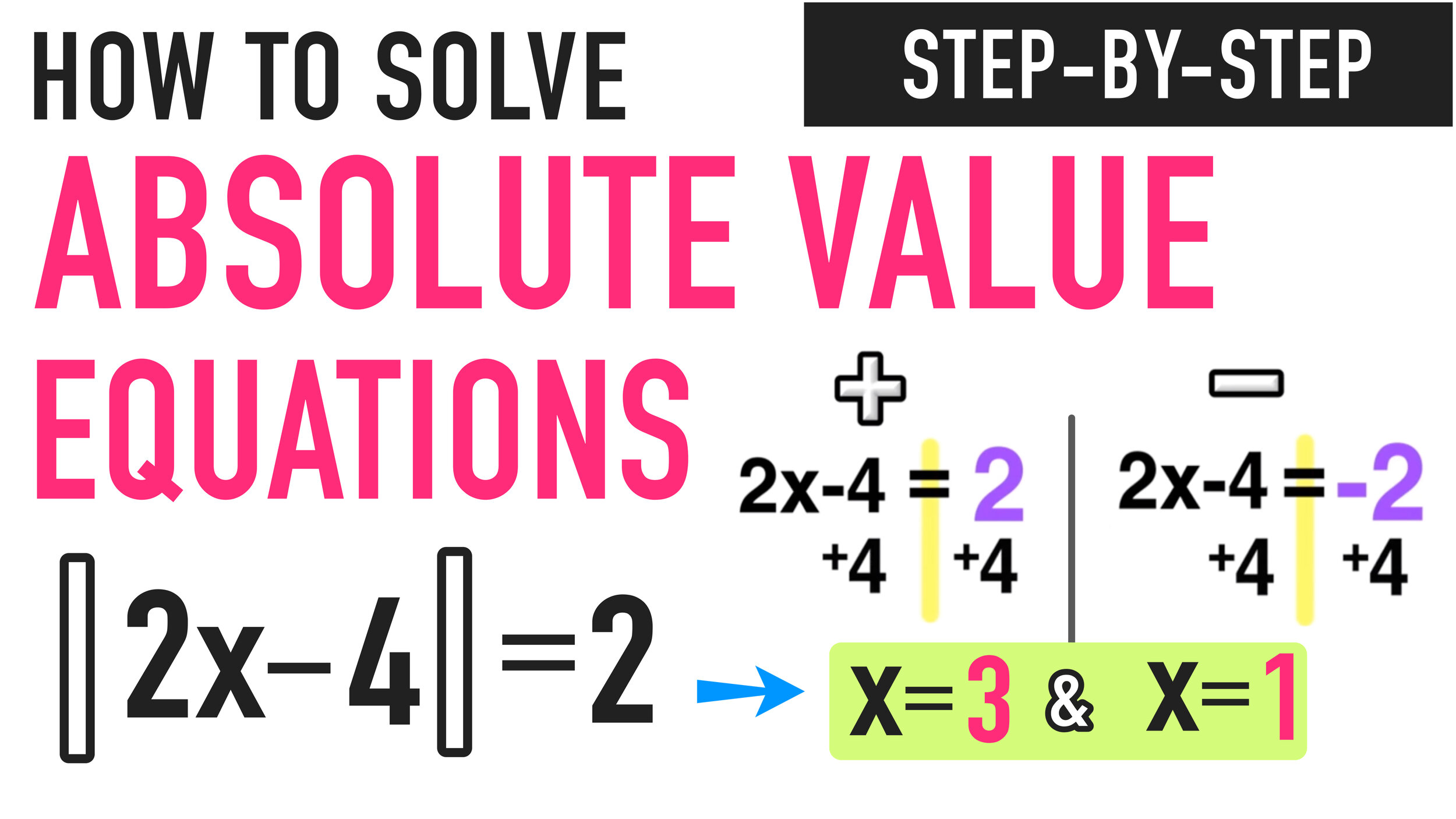
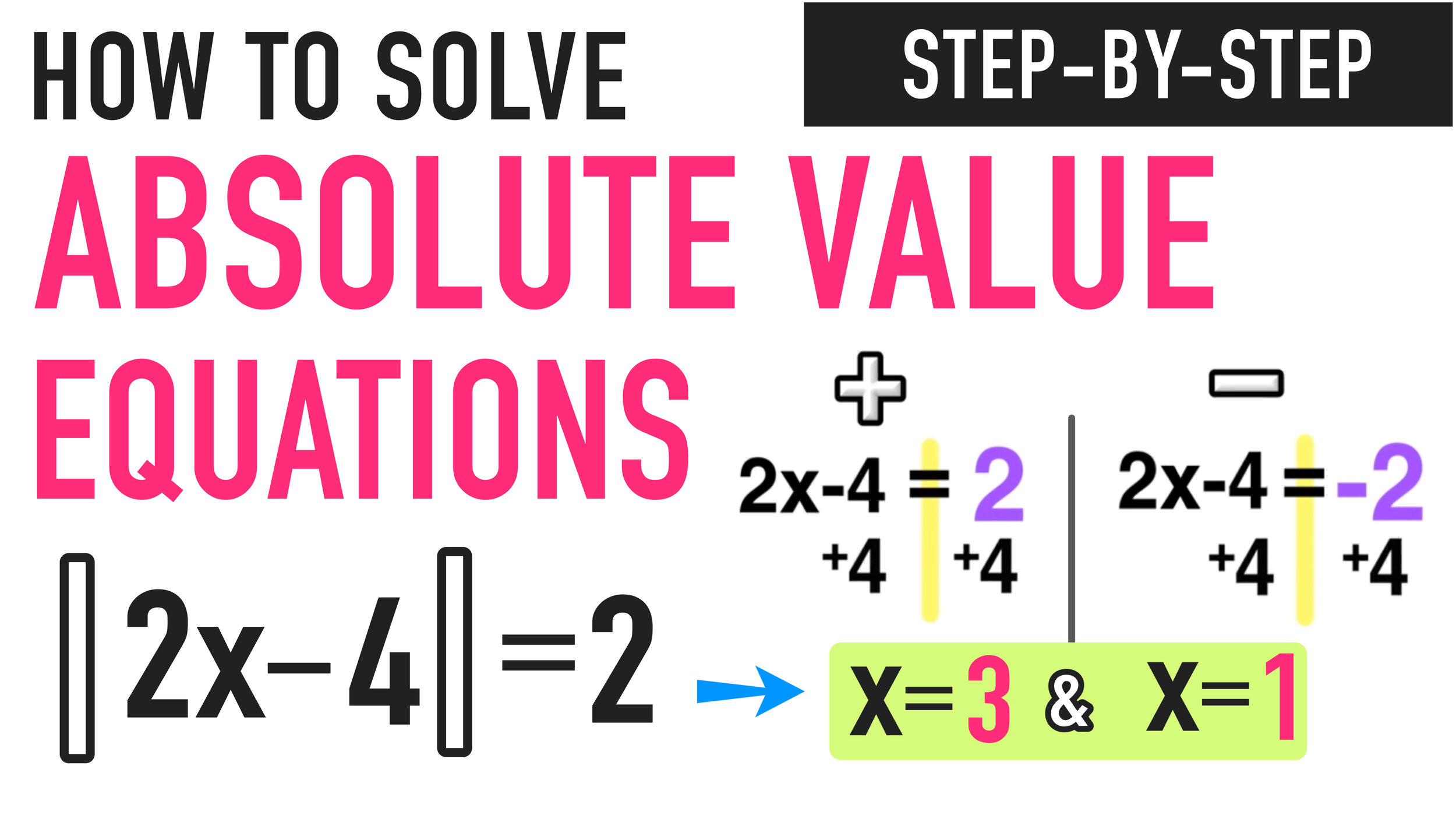
Welcome to this free lesson guide that accompanies this Solving Absolute Value Equations Tutorial where you will learn the answers to the following key questions and information:
This Complete Guide to Solving Absolute Value Equations includes several examples, a step-by-step tutorial and an animated video tutorial.
*This lesson guide accompanies our animated Solving Absolute Value Equations Explained! video.
Want more free math lesson guides and videos? Subscribe to our channel for free!
Fact: Any value inside of absolute value bars represents either a positive number or zero.
Notice that the absolute value graph in Figure 1 has a range of y is greater than or equal to 0 (it is never negative)
Furthermore, consider the example below:
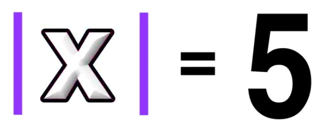
There are two values that would make this equation true!
The absolute value of 5 AND the absolute value of -5 both equal positive 5.
This should make sense when you graph the line y=5 over the absolute value function graph because you can see that there are two intersection points, and thus two solutions.
to two solutions!" width="466" height="303" />
Now you know that ABSOLUTE VALUE EQUATIONS CAN HAVE TWO SOLUTIONS.
Now you are ready to try a few examples.
are like terms." width="473" height="57" />
We will be using the following 3-step process that can be used to solve any absolute value equation:
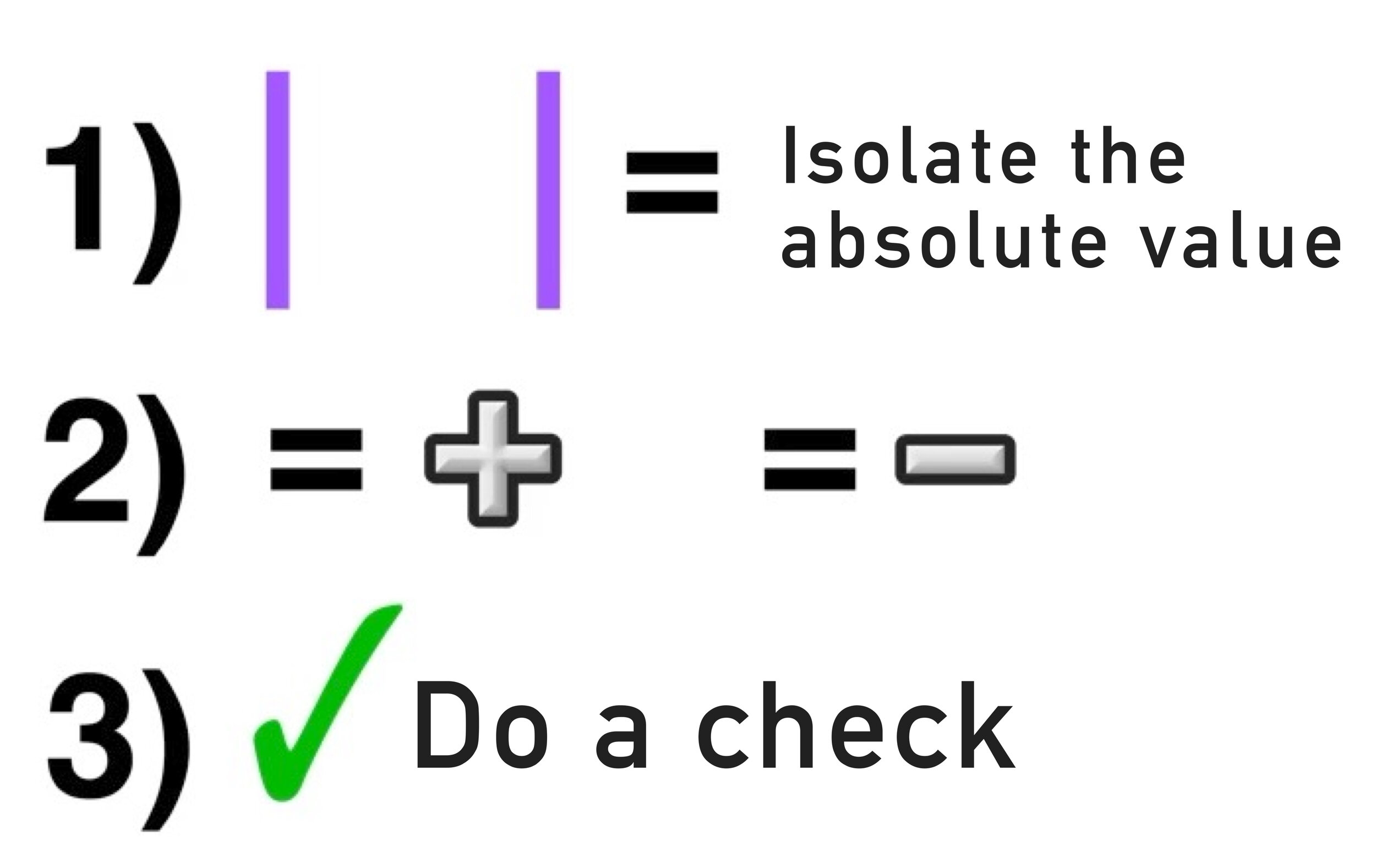
STEP ONE: Isolate the Absolute Value
In this example, the absolute value is already isolated on one side of the equals sign, which means that there are no other terms outside of the absolute value, so you can move onto step two.
STEP TWO: Solve for Positive AND Solve for Negative
For step two, you have to take the original equation |x+3| = 6 and split it up into two equations, one equal to POSITIVE 6 and the other equal to NEGATIVE 6. You also get rid of the absolute value bars.
